พบกันอีกครั้งกับ แอดมิน ADMIN JAMES DEAN หนึ่งในบ่ายวันจันทร์แบบนี้ วันนี้ผมจะขออนุญาตมาทำการโพสต์และแชร์ความรู้เกี่ยวกับเรื่อง การเตรียมตัวสอบเพื่อที่จะได้ใบประกอบวิชาชีพวิศวกรโยธา มาฝากเพื่อนๆ ทุกคนนะครับ
ขณะนี้ผมกำลังพาเพื่อนๆ ทบทวนเนื้อหาอยู่ภายในหัวข้อ การนำเอาวิธีการที่มีชื่อเรียกว่า วิธีการงานน้อยที่สุด หรือชื่อในภาษาอังกฤษว่า LEAST WORK METHOD ซึ่งถือได้ว่าวิธีการนี้เป็น CLASSICAL METHOD วิธีการหนึ่งเลยก็ว่าได้ โดยที่วิธีการนี้จะเป็นการต่อยอดนำเอาวิธี CASTIGLIANO’S 2’ND THEOREM มาประยุกต์ใช้งานสำหรับการแก้ปัญหางานวิศวกรรมโครงสร้างที่มีลักษณะเป็นแบบ STATICALLY INDETERMINATE ดังนั้นในวันนี้ผมจะขออนุญาตเริ่มต้นโดยทำการอธิบายวิธีในการประยุกต์ใช้วิธีการๆ นี้กับโครงสร้างประเภท คานรับแรงดัด หรือ BEAM BENDING โดยที่รายละเอียดของวิธีการนั้นจะเป็นดังต่อไปนี้ครับ
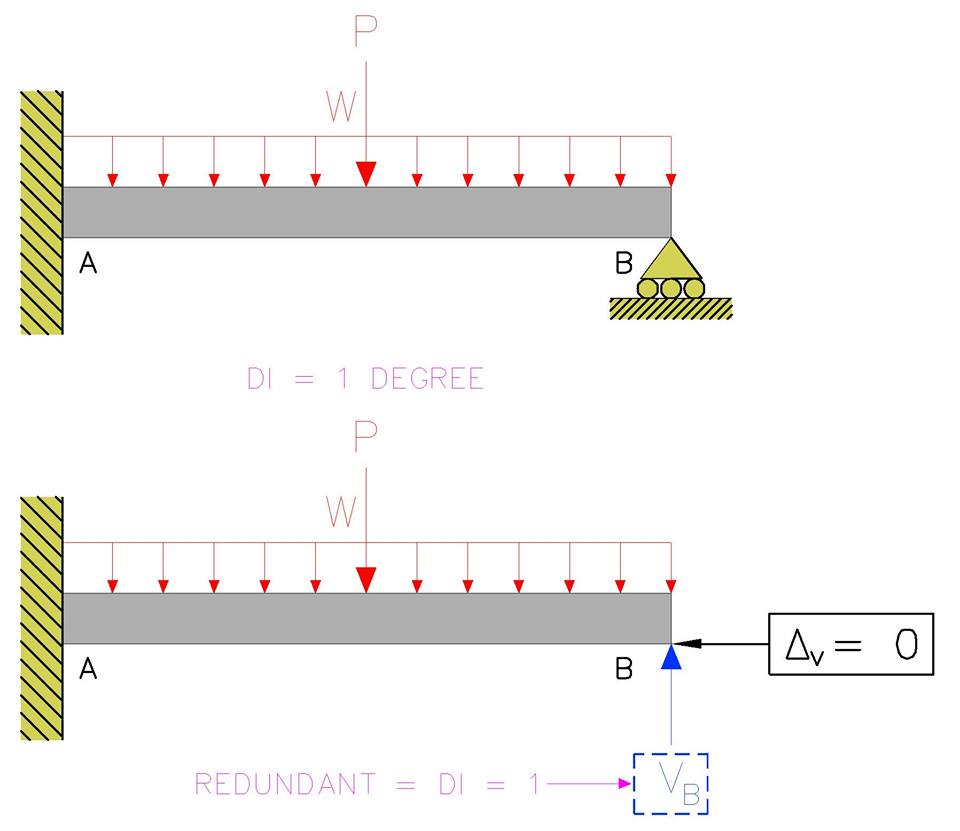
จากรูปๆ นี้เมื่อเราต้องการที่จะทำการวิเคราะห์โครงสร้างคานรับแรงดัดนี้ สิ่งแรกที่เราจะต้องทำคือ ทำการตรวจสอบ DEGREE OF INDETERMINACY หรือค่า DI ของระบบโครงสร้างคานรับแรงดัดนี้ออกมาให้ได้เสียก่อน จากนั้นพอเราทราบค่า DI เราก็จะทำการเลือก “ปลด” เทอมของ “แรงตัวเกิน” หรือ REDUNDANT ออกจนกว่าโครงสร้างนั้นๆ จะมีสภาพที่เป็น STATICALLY DETERMINATE STRUCTURE ผมย้ำนะครับว่าโครงสร้างจำเป็นที่จะต้องมีสภาพ STATICALLY DETERMINATE STRUCTURE อยู่พูดง่ายๆ คือต่อให้เราเลือกทำการปลด REDUNDANT ออกไปมากหรือน้อยเพียงใดก็แล้วแต่โครงสร้างนั้นๆ ยังคงจำเป็นที่จะต้องมีลักษณะที่มีเสถียรภาพเพียงพออยู่เสมอนะครับ
ทีนี้พอเราทำการปลด REDUNDANT ออกไปแล้วเราก็จะใส่แรงแทนที่ REDUNDANT นั้นๆ ให้อยู่ในรูปตัวแปรตัวแปรหนึ่งโดยที่จะทำการสมมติว่าทิศทางของแรงๆ นั้นจะเป็นไปในทิศทางที่แรงๆ นั้นควรที่จะเป็นครับ ตัวอย่างเช่น จากรูปๆ นี้หากเรามีความต้องการที่จะทำการแก้ปัญหาค่าแรงปฏิกิริยา ณ จุดรองรับ B ของโครงสร้างๆ นี้ซึ่งโดยมากแล้วแรงกระทำภายนอก หรือ EXTERNAL LOAD ของระบบนั้นจะเป็นไปในทิศทางลง ซึ่งจะส่งผลทำให้ค่าแรงปฏิกิริยา ณ จุดรองรับส่วนใหญ่นั้นเป็นไปในทิศทางตรงกันข้ามกับ EXTERNAL LOAD นั่นก็คือจะเป็นไปในทิศทางขึ้น เราก็อาจจะทำการสมมติว่าแรงกระทำที่ตำแหน่ง B นั้นเป็นไปในทิศทางขึ้น โดยต่อให้เราทำการสมมติผิดก็ไม่ได้เสียหายอะไร เพราะสุดท้ายพอทำการคำนวณเสร็จหากทิศทางที่เราได้ทำการสมมติเอาไว้ไม่ถูกต้องคำตอบก็จะฟ้องด้วยเครื่องหมายเองว่าทิศทางที่เราได้สมมติเอาไว้นั้นไม่ถูกต้อง เป็นต้นครับ
ต่อมาก็ให้ทำการวิเคราะห์หาแรง REACTIONS ต่างๆของโครงสร้าง โดยให้ถือว่าแรง REDUNDANT ที่สมมตินั้นเสมือนแรงๆ หนึ่งในระบบโครงสร้าง ดังนั้นค่า REACTIONS ต่างๆจะมีค่าของแรง REDUNDANT นี้รวมอยู่ด้วย
จากนั้นก็ให้เราทำการเขียนพจน์ของพลังงานค่าของความเครียด U ว่าโครงสร้างที่กำหนดให้นั้นจะมีผลจากการกระทำของแรงอะไรบ้างและก็ทำการหาค่าการเสียรูปต่างๆ โดยที่เทอมต่างๆ ก็จะเหมือนๆ กัน คือ การรวมผลต่างๆ (∑, ∫) ของผลคูณระหว่างค่าแรงในรูปแบบต่างๆ เช่น N (แรงตามแนวแกน) M (แรงดัด) V (แรงเฉือน) T (แรงบิด) เป็นต้น คูณกับค่า PARTIAL DERIVATIVE ของแรงนั้นๆ เทียบกับค่าแรง REDUNDANT และหารด้วยค่าความแข็งแกร่งของโครงสร้างที่มีต่อแรงนั้นๆ (RIGIDITY) ซึ่งก็จะสอดคล้องกับแรงที่เราทำการพิจารณาในพจน์นั้นๆ เช่น ในเทอมของแรงตามแนวแกน ค่า AXIAL RIGIDITY มีค่าเท่ากับ AE/L เทอมของแรงดัด ค่า FLEXURAL RIGIDITY มีค่าเท่ากับ EI เทอมของแรงเฉือน ค่า SHEAR RIGIDITY มีค่าเท่ากับ AG เทอมของแรงบิด ค่า TORSIONAL RIGIDITY มีค่าเท่ากับ GK เป็นต้น
ต่อมาเราก็เพียงแค่แทนค่าการเสียรูปโดยคำนึงจาก BOUNDARY CONDITIONS ของจุดรองรับที่เราได้เลือกให้เป็น REDUNDANT ว่ามีค่าเท่ากับเท่าใด ซึ่งโดยมากสำหรับจุดรองรับแบบ RIGID SUPPORTแล้วค่าการเสียรูปก็จะมีค่าเท่ากับ ศูนย์ และสุดท้ายคำตอบของค่าแรงปฏิกิริยาที่เราต้องการที่จะทราบคำตอบภายในโครงสร้างๆ หนึ่งนั้นก็จะสามารถหาได้จาก
0 = ∂U/∂P(REDUNDANT)
0 = ∑(N)[∂N/∂P(REDUNDANT)](L/AE) + ∑∫(M)[∂M/∂P(REDUNDANT)]/(EI)dx + ∑∫(λV)[∂V/∂P(REDUNDANT)]/(AG)dx + ∑∫(T)[∂T/∂P(REDUNDANT)]/(GK)dx+…
พอเราทำตามขั้นตอนข้างต้นทั้งหมดแล้วเสร็จเราก็จะได้ชุดสมการที่มีคำตอบเท่ากับ ศูนย์ เท่ากับจำนวนของ REDUNDANT ที่เราได้แทนเอาไว้ในโครงสร้าง เราก็เพียงแค่ทำการแก้ SIMULATNEOUS EQUATIONS ต่างๆ เพื่อที่จะทำการหาค่าคำตอบของ REDUNDANT เหล่านั้นออกมา จากนั้นเราก็ค่อยนำค่าคำตอบเหล่านี้ไปทำการคำนวณหาค่าแรงภายในหรือ INTERNAL FORCE ต่างๆ ภายในระบบโครงสร้างของเราต่อไปนั่นเองครับ
เป็นยังไงบ้างครับ ง่ายมากๆ เลยใช่มั้ยละครับ? หากอ่านที่ผมอธิบายแล้วไม่เข้าใจตรงไหนก็ไม่เป็นไรนะครับ เอาเป็นว่าในครั้งหน้าที่เราพบกัน ผมจะค่อยๆ ทำตัวอย่างในการวิเคราะห์โครงสร้างแต่ละชนิดให้ทุกๆ ท่านได้รับชมกันก็แล้วกันนะครับ ไม่ว่าจะเป็น โครงสร้างโครงข้อหมุน (TRUSS FRAMING) โครงสร้างคานรับแรงดัด (BEAM BENDING) และโครงสร้างโครงข้อแข็ง (RIGID FRAME) ยังไงเพื่อนๆ ท่านใดที่มีความสนใจในหัวข้อๆ นี้เป็นพิเศษก็อย่าลืมติดตามกันได้นะครับ
หวังว่าความรู้เล็กๆ น้อยๆ ที่ผมได้นำมาฝากแก่เพื่อนๆ ทุกๆ ท่านในวันนี้จะมีประโยชน์ต่อทุกๆ ท่านไม่มากก็น้อย และ จนกว่าจะพบกันใหม่นะครับ
Bhumisiam ภูมิสยาม
ผู้ผลิตรายแรก Spun Micro Pile
1) ได้รับการรับรองระบบบริหารงานคุณภาพ ตามมาตรฐาน ISO 9001:2015
2) ได้รับมาตรฐาน ISO 9001:2015 UKAS ภายใต้การดูแลของ อังกฤษ
3) ได้รับมาตรฐาน ISO 9001:2015 NAC ภายใต้การดูแลของ สมอ.
4) ได้รับมาตรฐาน มอก. 397-2524 เสาเข็ม Spun MicroPile Dia 21, 25, 30 cm.
5) ผู้ผลิต Spun MicroPile ที่ได้รับ Endorsed Brand รับรองคุณภาพมาตรฐานจาก SCG
6) ผู้นำระบบ Computer ที่ทันสมัยผลิต เสาเข็ม Spun MicroPile
7) ลิขสิทธิ์เสาเข็ม Spun MicroPile
8) เทคโนโลยีการผลิต จากประเทศเยอรมัน
9) ผู้ผลิต Spun MicroPile แบบ “สี่เหลี่ยม”
10) การผลิตคอนกรีตและส่วนผสม ใช้ Program SCG-CPAC
เสาเข็ม สปันไมโครไพล์ ช่วยแก้ปัญหาได้เพราะ?
1) สามารถทำงานในที่แคบได้
2) ไม่ก่อให้เกิดมลภาวะทางเสียง
3) หน้างานสะอาด ไม่มีดินโคลน
4) สามารถรับน้ำหนักได้ 20-50 ตัน/ต้น ขึ้นอยู่กับสภาพชั้นดินแต่ละพื้นที่
5) สามารถตอกชิดกำแพง ไม่ก่อให้โครงสร้างเดิมเสียหาย
Mr.MicroPile
สนใจติดต่อสินค้า เสาเข็มสปันไมโครไพล์ มาตรฐาน มอก. โทร
063-889-7987
082-790-1447
082-790-1448
082-790-1449