สวัสดีครับแฟนเพจที่รักทุกๆ ท่าน
พบกันอีกครั้งหนึ่งในบ่ายวันจันทร์แบบนี้ วันนี้ผมจะขออนุญาตมาทำการโพสต์และแชร์ความรู้เกี่ยวกับเรื่อง การเตรียมตัวสอบเพื่อที่จะได้ใบประกอบวิชาชีพวิศวกรโยธา มาฝากเพื่อนๆ ทุกคนนะครับ
วันนี้ผมจะขออนุญาตมาพูดถึงเรื่อง วิธีในการวิเคราะห์โครงสร้างด้วยวิธีการที่มีความทันสมัยใหม่ หรือ ADVANCED STRUCTURAL ANALYSIS METHOD โดยวิธีการนี้ก็คือ วิธีการวิเคราะห์ด้วยเมตริกซ์ หรือ MATRIX ANALYSIS METHOD ซึ่งเป็นวิธีการที่ได้รับการพัฒนามาจากการอาศัยหลักการทางด้าน FINITE ELEMENT ANALYSIS นั่นเองครับ
อย่างที่ผมได้เรียนเพื่อนๆ ไปก่อนหน้านี้ว่าวิธีการ MATRIX DISPLACEMENT METHOD นั้นจะได้รับความนิยมมากกว่าวิธีการ MATRIX FORCE METHOD ดังนั้นในวันนี้ผมจะขอเริ่มต้นอธิบายถึงขั้นตอนโดยสังเขปคร่าวๆ ของการวิเคราะห์โครงสร้างโดยวิธีการ MATRIX DISPLACEMENT METHOD และหากมีเวลาเหลือจริงๆ ผมก็จะขออนุญาตย้อนมาพูดถึงเรื่องวิธีการ MATRIX FORCE METHOD เพื่อที่เพื่อนๆ ทุกคนจะได้มีความรู้พื้นฐานของวิธีการๆ นี้ติดตัวเอาไว้บ้าง เผื่อเอาไว้ว่าเพื่อนๆ อาจจะมีโอกาสได้นำไปใช้งานในกรณีใดกรณีหนึ่งนั่นเอง ซึ่งรายละเอียดของขั้นตอนต่างๆ ในการวิเคราะห์โครงสร้างด้วยวิธีการ MATRIX DISPLACEMENT METHOD นั้นจะประกอบไปด้วยขั้นตอนหลักๆ ทั้งหมด 11 ขั้นตอนดังต่อไปนี้ครับ
- เริ่มต้นโดยการที่เราจะทำการกำหนดหมายเลขของ จุดต่อ หรือ NODE และ ชิ้นส่วน หรือ ELEMENT ที่มีอยู่ภายในระบบโครงสร้างเสียก่อน ทั้งนี้ก็เพื่อที่จะได้สามารถอ้างอิงถึงได้อย่างถูกต้องและเพื่อไม่เกิดความสับสนนะครับ
- เราจะต้องทำการสร้างเมตริกซ์ที่มีความสำคัญมากตัวหนึ่งขึ้นมาก่อนนั่นก็คือ เมตริกซ์ความแข็งแกร่ง ของ ชิ้นส่วน ที่อ้างอิงตามแกนของ ชิ้นส่วนของโครงสร้าง หรือ MEMBER STIFFNESS MATRIX ซึ่งในที่นี้ผมจะแทนให้อยู่อยู่ในรูปของเมตริกซ์ [km] โดยหากเพื่อนๆ ติดตามมาโดยตลอดก็น่าที่จะจำได้ว่าผมเคยอธิบายถึงเรื่องๆ นี้ไปบ้างพอสังเขปก่อนหน้านี้แล้ว ยังไงหากเพื่อนๆ สนใจสามารถที่จะไปลองหาคลิปย้อนหลังดูกันได้นะครับ
- เราจะใช้ความสัมพันธ์ของค่า แรง หรือ FORCE และ การเปลี่ยนตำแหน่ง หรือ DEFORMATION เพื่อที่จะทำการคำนวณหาความสัมพันธ์ระหว่างค่า แรงภายใน ที่เกิดขึ้นในชิ้นส่วนของโครงสร้าง ซึ่งในที่นี้ผมจะแทนให้อยู่อยู่ในรูปของเมตริกซ์ {f} กับค่า การเปลี่ยนแปลงรูปร่างของชิ้นส่วนโครงสร้าง ซึ่งในที่นี้ผมจะแทนให้อยู่อยู่ในรูปของเมตริกซ์ {d} ทั้งนี้หมายเหตุไว้ตรงนี้ด้วยนะครับว่าสำหรับเมตริกซ์ {d} นั้นเราจะทำการกำหนดให้ผลต่างๆ ของโครงสร้างนั้นอาศัย ระบบแกนอ้างอิงของชิ้นส่วนของโครงสร้าง หรือ LOCAL COORDINATE SYSTEM ซึ่งเราอาจจะสามารถเรียกกระบวนการนี้ได้ว่าเป็น FORCE-DISPLACEMENT RELATIONSHIP โดยในที่สุดเราก็อาจจะสามารถเขียนความสัมพันธ์ต่างๆ เหล่านี้ให้อยู่ในรูปแบบสมการเมตริกซ์อย่างเป็นทางการได้ว่า
{f} = [km] {d}
- เราจะใช้ สมการความสอดคล้อง หรือ COMPATIBILTY EQUATION หรือ เงื่อนไขของความสอดคล้อง หรือ COMPATIBILTY CONDITION เพื่อที่จะเขียนความสัมพันธ์ของการเปลี่ยนแปลงรูปร่างของชิ้นส่วนโครงสร้าง {d} กับ การเปลี่ยนตำแหน่งที่จุดต่อ หรือ NODAL DISPLACEMENT ของชิ้นส่วนของโครงสร้าง {D} ทั้งนี้หมายเหตุไว้ตรงนี้ด้วยนะครับว่าสำหรับเมตริกซ์ {D} นั้นเราจะทำการกำหนดให้ผลต่างๆ ของโครงสร้างนั้นอาศัย ระบบแกนอ้างอิงของระบบของโครงสร้าง หรือ GLOBAL COORDINATE SYSTEM ทั้งนี้เราก็จะทำให้เราได้เมตริกซ์เพิ่มขึ้นมาอีกเมตริกซ์หนึ่งที่มีความสำคัญนั่นก็คือ เมตริกซ์แปลงค่าการเสียรูป หรือ DISPLACEMENT TRANSFORMATION MATRIX ซึ่งในที่นี้ผมจะแทนให้อยู่อยู่ในรูปของเมตริกซ์ [T] โดยในที่สุดเราก็อาจจะสามารถเขียนความสัมพันธ์ต่างๆ เหล่านี้ให้อยู่ในรูปแบบสมการเมตริกซ์อย่างเป็นทางการได้ว่า
{d} = [T] {D}
- เราจะอาศัยสมการความสมดุลที่จุดต่อหรือ NODAL EQUILIBRIUM EQUATION เพื่อหาความสัมพันธ์ระหว่างแรงกระทำ {F} ทั้งนี้หมายเหตุไว้ตรงนี้ด้วยนะครับว่าสำหรับเมตริกซ์ {F} นั้นเราจะทำการกำหนดให้ผลต่างๆ ของโครงสร้างนั้นอาศัย ระบบแกนอ้างอิงของระบบของโครงสร้าง หรือ GLOBAL COORDINATE SYSTEM กับค่าแรงภายในที่เกิดขึ้นในชิ้นส่วนของโครงสร้าง {f} ที่เราได้หาไว้ก่อนหน้านี้แล้ว โดยในที่สุดเราก็อาจจะสามารถเขียนความสัมพันธ์ต่างๆ เหล่านี้ให้อยู่ในรูปแบบสมการเมตริกซ์อย่างเป็นทางการได้ว่า
{F} = [T]^(T) {f}
หมายเหตุไว้ตรงนี้ด้วยนะครับว่าสำหรับเมตริกซ์ [T]^(T) ก็คือ เมตริกซ์แปลงแรง หรือ FORCE TRANSFORMATION MATRIX นะครับ
- เราจะหาความสัมพันธ์ของ แรงภายใน ที่เกิดขึ้นภายในชิ้นส่วนต่างๆ ของโครงสร้างกับค่าต่างๆ ของ การเปลี่ยนตำแหน่งที่จุดต่อ ดังนั้นเราก็จะสามารถทำได้โดยการแทนค่าเมตริกซ์ที่ได้สร้างเอาไว้ในข้อที่ 3 ซึ่งจะมีค่าเท่ากับ
{f} = [km] {d}
เข้าไปด้วยเมตริกซ์ที่ได้สร้างเอาไว้ในข้อที่ 4
{d} = [T] {D}
ดังนั้นก็จะได้ว่า
{f} = [km] [T] {D}
- เราจะหาความสัมพันธ์ของ แรงภายนอก ที่เกิดขึ้นภายในระบบของโครงสร้างกับค่าต่างๆ ของ การเปลี่ยนตำแหน่งที่จุดต่อ ดังนั้นเราก็จะสามารถทำได้โดยการแทนค่าเมตริกซ์ที่ได้สร้างเอาไว้ในข้อที่ 5 ซึ่งจะมีค่าเท่ากับ
{F} = [T]^(T) {f}
เข้าไปด้วยเมตริกซ์ที่ได้สร้างเอาไว้ในข้อที่ 6
{f} = [km] [T] {D}
ดังนั้นก็จะได้ว่า
{F} = [T]^(T) [km] [T] {D}
- ซึ่งตรงนี้เองที่เราจะสามารถสร้าง เมตริกซ์ความแข็งแกร่ง ของ ชิ้นส่วน ที่อ้างอิงตามแกนของ ระบบของโครงสร้าง หรือ STRUCTURAL GLOBAL STIFFNESS MATRIX ซึ่งในที่นี้ผมจะแทนให้อยู่อยู่ในรูปของเมตริกซ์ [k] ก็แล้วกัน ทั้งนี้ค่าเมตริกซ์ [k] นี้จะมีค่าเท่ากับ
[k] = [T]^(T) [km] [T]
ดังนั้นหากเราทำการแทนค่าเมตริกซ์ [k] ข้างต้นนี้ลงไปในเมตริกซ์ในข้อที่ 7 ก็จะทำให้ได้เมตริกซ์ของแรงภายนอกที่ถูกจัดรูปเสียใหม่ ซึ่งก็จะมีค่าเท่ากับ
{F} = [k] {D}
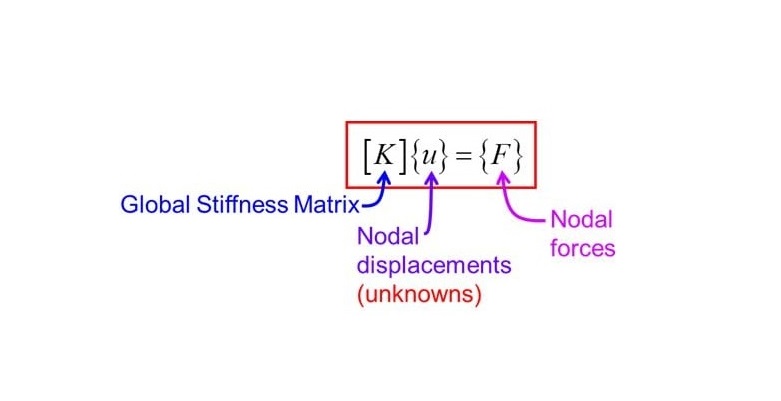
- เราจะทำการจัดรูปและรวมเมตริกซ์ความแข็งแกร่งของโครงสร้างทั้งระบบออกมา ซึ่งในที่สุดก็จะได้ค่าเมตริกซ์ความแข็งแกร่งค่าสุดท้ายนั่นก็คือ เมตริกซ์ความแข็งแกร่ง ของ ระบบของโครงสร้าง หรือ STRUCTURAL STIFFNESS MATRIX ซึ่งในที่นี้ผมจะแทนให้อยู่อยู่ในรูปของเมตริกซ์ [K] ก็แล้วกัน ซึ่งพอทำการแทนลงไปในเมตริกซ์ที่เราได้สร้างเอาไว้ในข้อที่ 8 ก็จะได้เป็นเมตริกซ์ของแรงภายนอกของโครงสร้างทั้งระบบออกมาเป็นที่เรียบร้อยแล้วซึ่งก็จะมีค่าเท่ากับ
{F} = [K] {D}
- ขั้นตอนนี้จะเป็นขั้นตอนของการหาคำตอบแล้ว โดยจะเริ่มต้นจากการจัดรูปเมตริกซ์ที่ได้ทำไว้ในข้อที่ 9 เพื่อที่จะใช้ทำการคำนวณหาค่า การเปลี่ยนตำแหน่งที่จุดต่อ ของโครงสร้างออกมาให้เราได้ทราบเสียก่อน ดังนั้นค่าเมตริกซ์ {D} ก็จะสามารถทำการคำนวณออกมาได้เท่ากับ
{D} = [K]^(-1) {Q}
- ขั้นตอนนี้เป็นขั้นตอนสุดท้ายนั่นก็คือ เราจะทำการคำนวณหาค่าเมตริกซ์ {f} หรือ ค่าแรงภายในต่างๆ ของชิ้นส่วนต่างๆ ของโครงสร้างออกมา ดังนั้นเราก็จะทำการแทนค่าเมตริกซ์ {D} ที่หาได้จากในข้อที่ 10 ลงไปในเมตริกซ์ที่ได้สร้างเอาไว้ในข้อที่ 6 ซึ่งจะมีค่าเท่ากับ
{f} = [km] [T] {D}
เพียงเท่านี้ก็จะทำให้เราสามารถที่จะหาคำตอบของเมตริกซ์ {f} ซึ่งเป็นเมตริกซ์แรงภายในทั้งหมดของชิ้นส่วนโครงสร้างแล้วละครับ
ในครั้งต่อไปที่เราจะมาพบกัน ผมจะขออนุญาตมาทำการยกตัวอย่างถึงปัญหาสักหนึ่งข้อที่จะอาศัย MATRIX DISPALCEMENT METHOD เป็นวิธีในการที่เราจะทำการวิเคราะห์โครงสร้าง ทั้งนี้ก็เพื่อที่เพื่อนๆ ทุกคนจะได้นึกภาพวิธีในการทำตามที่ผมได้อธิบายด้วยคำพูดไปในโพสต์ๆ นี้ตามกันออก หากว่ามีเพื่อนๆ ท่านใดที่สนใจเป็นพิเศษในบทความๆ นี้ของผม ก็สามารถที่จะติดตามรับชมกันได้ในสัปดาห์หน้าครับ
ผมหวังว่าความรู้เล็กๆ น้อยๆ ที่ผมได้นำมาฝากแก่เพื่อนๆ ทุกๆ ท่านในวันนี้จะมีประโยชน์ต่อทุกๆ ท่านไม่มากก็น้อย และ จนกว่าจะพบกันใหม่นะครับ
#การเตรียมตัวสอบเพื่อที่จะได้ใบประกอบวิชาชีพวิศวกรโยธา
#AdvancedStructuralAnalysisMethod
#MatrixAnalaysis03
#IntroductionToMatrixDisplacementMethod01
ADMIN JAMES DEAN
บริษัท ภูมิสยาม ซัพพลาย จำกัด ผู้นำกลุ่มธุรกิจเสาเข็มสปัน ไมโครไพล์ รายแรกและรายเดียวในประเทศไทย ที่ได้การรับรองมาตรฐาน ISO 45001:2018 การจัดการอาชีวอนามัยและความปลอดภัย การให้บริการตอกเสาเข็ม The Provision of Pile Driving Service และได้รับการรับรอง ISO 9001:2015 ของระบบ UKAS และ NAC รายแรกและรายเดียวในประเทศไทย ที่ได้รับการรับรองระบบบริหารงานคุณภาพ ตามมาตรฐานในกระบวนการ การออกแบบเสาเข็มสปันไมโครไพล์ การผลิตเสาเข็มสปันไมโครไพล์ และบริการตอกเสาเข็มเสาเข็มสปันไมโครไพล์ (Design and Manufacturing of Spun Micropile/Micropile and Pile Driving Service) Certified by SGS (Thailand) Ltd.
บริษัท ภูมิสยาม ซัพพลาย จำกัด คือผู้ผลิตรายแรกและรายเดียวในไทย ที่ได้รับการรับรองคุณภาพ Endoresed Brand จาก SCG ด้านการผลิตเสาเข็ม สปันไมโครไพล์ และได้รับเครื่องหมาย มาตรฐาน อุตสาหกรรม มอก. 397-2524 เสาเข็มสปันไมโครไพล์ Spun Micro Pile พร้อมรับประกันผลงาน และความเสียหายที่เกิดจากการติดตั้ง 7+ Year Warranty เสาเข็มมีรูกลมกลวงตรงกลาง การระบายดินทำได้ดี เมื่อตอกแล้วแรงสั่นสะเทือนน้อยมาก จึงไม่กระทบโครงสร้างเดิม หรือพื้นที่ข้างเคียง ไม่ต้องขนดินทิ้ง ตอกถึงชั้นดินดานได้ ด้วยเสาเข็มคุณภาพมาตรฐาน มอก. การผลิตที่ใช้เทคโนโลยีที่ทันสมัย จากประเทศเยอรมัน เสาเข็มสามารถทำงานในที่แคบได้ หน้างานสะอาด ไม่มีดินโคลน เสาเข็มสามารถรับน้ำหนักปลอดภัยได้ 15-50 ตัน/ต้น ขึ้นอยู่กับขนาดเสาเข็มและสภาพชั้นดิน แต่ละพื้นที่ ทดสอบโดย Dynamic Load Test ด้วยคุณภาพและการบริการที่ได้มาตรฐาน เสาเข็มเราจึงเป็นที่นิยมในงานต่อเติม
รายการเสาเข็มภูมิสยาม
1. สี่เหลี่ยม S18x18 cm.
รับน้ำหนัก 15-20 ตัน/ต้น
2. กลม Dia 21 cm.
รับน้ำหนัก 20-25 ตัน/ต้น
3. กลม Dia 25 cm.
รับน้ำหนัก 25-35 ตัน/ต้น
4. กลม Dia 30 cm.
รับน้ำหนัก 30-50 ตัน/ต้น
(การรับน้ำหนักขึ้นอยู่กับสภาพชั้นดินในแต่ละพื้นที่)
☎ สายด่วนภูมิสยาม:
082-790-1447
082-790-1448
082-790-1449
091-947-8945
081-634-6586
? Web:
bhumisiam.com
micro-pile.com
spun-micropile.com
microspunpile.com
bhumisiammicropile.com