สวัสดีครับแฟนเพจที่รักทุกๆ ท่าน
ในวันนี้ผมยังจะขออนุญาตมาทำการโพสต์และแชร์ความรู้เกี่ยวกับเรื่อง ปัญหาและเทคนิคในการทำงานก่อสร้างโครงสร้างประเภทต่างๆ อยู่นะครับ
เนื่องจากเมื่อเย็นของเมื่อวานนี้ได้มีน้องนักศึกษาท่านหนึ่งได้อินบ็อกซ์เข้ามาปรึกษาผมและได้แจ้งว่าอยากจะรบกวนให้ช่วยอธิบายและแสดงวิธีในการแก้ปัญหาในกรณีที่โครงสร้างๆ คานยื่นโครงสร้างหนึ่งซึ่งมีรูปทรงแปลกๆ ดังรูปที่แสดง นั่นก็คือค่าความสูงของหน้าตัดจะมีค่าไม่คงที่ตลอดความยาวของคานนั่นเอง ซึ่งน้องได้แจ้งว่าต้องนำเอาคำตอบไปใช้ค่อนข้างด่วนซึ่งเรียนตามตรงผมไม่อยากที่จะสนับสนุนให้น้องทำแบบนี้เท่าใดนักเพราะเกรงว่าจะทำให้พวกเราหลายๆ คนเอาเยี่ยงอย่างได้แต่เอาเป็นว่าผมทำให้ครั้งนี้เป็นกรณีพิเศษก็แล้วกันเพราะเห็นว่าน้องมีความจำเป็นต้องนำคำตอบในคำถามข้อนี้ไปใช้ในโครงงานปริญญานิพนธ์ของน้อง เอาเป็นว่าเรามาดูรายละเอียดของคำถามกันเลยดีกว่านะครับ
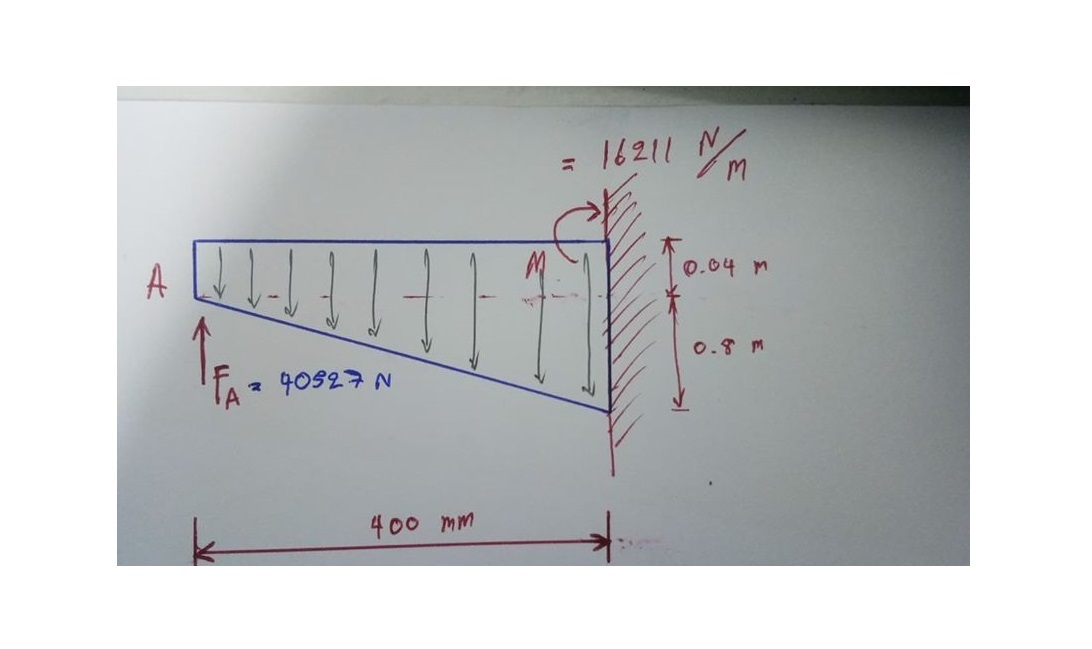
มีคานยื่นที่มีความยาวของช่วงยื่นเท่ากับ 400 มม หรือ 40 ซม หรือ 0.40 เมตร ซึ่งถือว่าเป็นคานที่มีความยาวของช่วงยื่นที่สั้นมากๆ คานๆ นี้จะมีความกว้างของหน้าตัดที่เท่าๆ กันตลอดทั้งความยาวของคานเท่ากับ 20 มม โดยที่ปลายยื่นจะมีความลึกของหน้าตัดเท่ากับ 40 มม จากนั้นหน้าตัดก็จะค่อยๆ ลาดชันลงไปจนมีขนาดของหน้าตัดที่ปลายด้านที่ติดกันกับจุดรองรับแบบยึดแน่น จะทำให้ความลึกของหน้าตัดในส่วนนี้มีค่าเท่ากับ 840 มม น้องแจ้งมาว่าค่าโมดูลัสยืดหยุ่นมีค่าเท่ากับ 210000 N/mm^(2) คำถามก็คือ ค่าการเสียรูปที่ปลายของคานยื่นคานนี้จะมีค่าเท่ากับเท่าใด ?

ปล 1
เนื่องจากผมพิจารณาดูแล้วจะพบว่าหากจะทำการอธิบายปัญหาข้อนี้ให้ครบถ้วนกระบวนความจริงๆ จะต้องใช้เนื้อที่ในการโพสต์ค่อนข้างที่จะยืดยาวมากๆ ผมจึงจะขอแบ่งการโพสต์ออกเป็นส่วนๆ ก็แล้วกันนะครับ
ปล 2
ภายหลังจากการพิจารณาเรื่องรูปทรงและขนาดต่างๆ ของคานยื่นคานนี้ก็จะพบว่า ค่าน้ำหนักของตัวคานเองนั้นจะมีค่าที่น้อยมากๆ ผมจึงเลือกทำการไม่สนใจค่าน้ำหนักบรรทุกของตัวโครงสร้างไปนะครับ
ก่อนอื่นเลยผมขอลองถามความเห็นจากเพื่อนๆ ในเพจก่อนนะครับว่า หากเราจะนำเอาวิธีการ CASTIGLIANO’S 2ND THEOREM มาใช้ในการวิเคราะห์โครงสร้างเพื่อที่จะทำการคำนวณหาค่าการเสียรูปที่ปลายคานยื่นนี้จะได้หรือไม่ ?
คำตอบคือ ได้ แต่ คำตอบที่ได้จากการคำนวณนั้นจะมีความใกล้เคียงกันกับค่าความเป็นจริงมากหรือน้อยแค่ไหนนั้นก็จะขึ้นอยู่กับเทอมต่างๆ ที่เรานำมาใช้ในการพิจารณาตอนที่เรานั้นทำการวิเคราะห์โครงสร้างนั่นเองครับ
โดยที่ในวันนี้ผมจะทำการคำนวณโดยวิธีการเหมือนที่เคยทำให้เพื่อนๆ ดูทุกๆ ครั้งก่อนหน้านี้นั่นก็คือ นำผลเฉพาะเทอมที่เป็น แรงดัด มาใช้ในการพิจารณาตอนที่เรานั้นทำการวิเคราะห์โครงสร้าง ซึ่งผมออกตัวไว้ก่อนตรงนี้เลยว่าคำตอบที่ได้จากการทำเช่นนี้สำหรับปัญหาข้อนี้จะผิดโดยสิ้นเชิง !!!
ใช่ครับ อ่านไม่ผิด “ผิดอย่างสิ้นเชิง” ทำไมน่ะหรอครับ ก็เพราะว่าหากเพื่อนๆ สังเกตดูดีๆ ก็จะพบว่าลักษณะของความยาวและรูปร่างของคานยื่นคานนี้จะค่อนข้างแปลกๆ นั่นก็คือ คานจะมีช่วงความยาวที่ค่อนข้าง สั้น แต่ ก็จะมีขนาดของความลึกของคานที่ค่อนข้างจะ มาก นะครับ
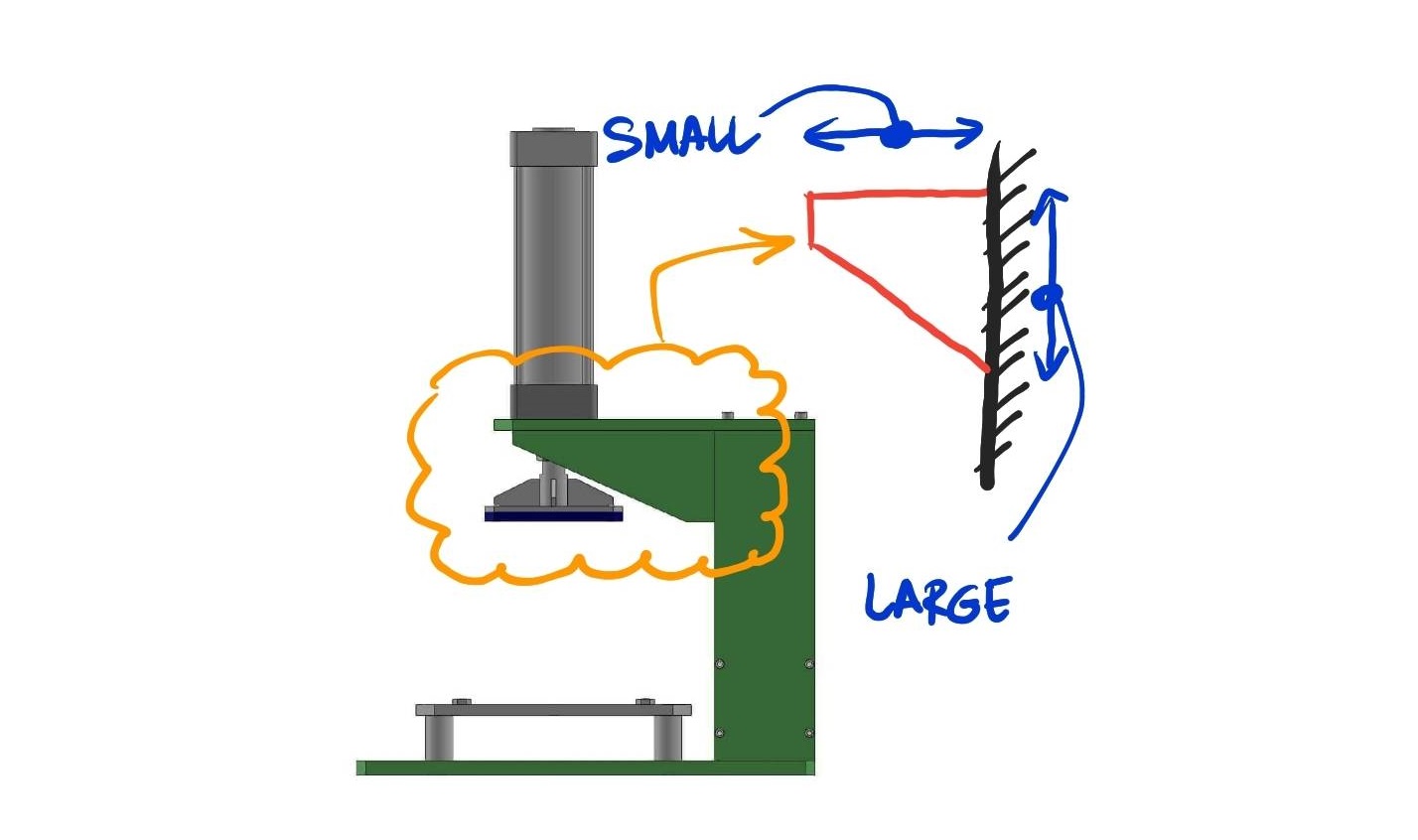
พุดมาถึงตรงนี้ผมเชื่อว่าคงจะมีเพื่อนของเราหลายๆ คนถึงบางอ้อแล้ว … ถูกต้องครับ คานๆ นี้จะมีลักษณะคล้ายๆ กันกับโครงสร้างจำพวกแป้นหูช้างหรือ CORBEL ซึ่งโครงสร้างแบบนี้เพื่อนๆ คงจะทราบกันดีอยู่แล้วว่าโครงสร้างประเภทนี้ก็คือโครงสร้างที่มีความวิกฤติต่อ แรงเฉือนโดยตรง หรือ DIRECT SHEAR นั่นเอง
พูดให้เข้าใจได้ง่ายๆ ก็คือ คานยื่นคานนี้จะได้รับผลจากการเสียรูปอันเนื่องจากแรงเฉือนมากกว่าผลจากแรงดัด ดังนั้นหากว่าเราไม่นำค่าของแรงเฉือนรวมเข้าไปในการวิเคราะห์โครงสร้างด้วย คำตอบที่ได้ก็จะผิดเพี้ยนออกไปอย่างแน่นอนนั่นเองครับ
ไม่เป็นไรนะครับ วันนี้เราจะมาดูผลของการวิเคราะห์โครงสร้างกรณีที่เราไม่นำผลจากการเสียรูปอันเนื่องมาจากแรงเฉือนมาคิดคำนึงถึงกันก่อนก็แล้วกันนะครับ
เรามาเริ่มต้นการคำนวณที่ค่าที่มีความสำคัญที่สุดก่อนนั่นก็คือ ค่าโมเมนต์ความเฉื่อยของหน้าตัด เพราะเมื่อคานมีลักษณะของหน้าตัดที่มีค่าของความลึกที่ไม่คงที่ก็จะส่งผลทำให้ค่าโมเมนต์ความเฉื่อยของหน้าตัดมีค่าไม่คงที่ตามไปด้วย ค่าความกว้างของคานยื่นนี้จะมีค่าคงที่ตลอดทั้งความยาวของคาน ทำให้ค่า B จะมีค่าเท่ากับ 20 มม ซึ่งเราสามารถที่จะใช้หลักการของตรีโกณมิติในการคำนวณหาค่าความสูงของหน้าตัดที่ขึ้นอยู่กับระยะทาง หรือ Hx ได้ ซึ่งสำหรับปัญหาข้อนี้ค่า H(x) ก็จะมีค่าเท่ากับ
H(x) = 40 + 2x
ดังนั้นในเมื่อคานๆ นี้เป็นคานรูปทรงสี่เหลี่ยมผืนผ้า ค่าโมเมนต์ความเฉื่อยจึงมีค่าเท่ากับ
I = I(x)
I(x) = B x H(x)^(3) /12
I(x) = 20 x (40 + 2x)^(3) /12
I(x) = 40 x (20 + x)^(3) / 3
จากนั้นเราก็ทำตามขั้นตอนตามปกติตามวิธีการของ CASTIGLIANO’S 2ND THEOREM ได้เลย ซึ่งค่าสมการโมเมนต์ดัดในระหว่างช่วง A ถึง B นั้นจะมีเพียง 1 สมการ นั่นก็คือ
M(AB) = Qx
ดังนั้นจะทำให้เทอม PARTIAL DIFFERENTIATE สมการโมเมนต์ดัดเทียบกับค่า Q ก็จะมีค่าเท่ากับ x ซึ่งพอเทอมทั้งสองนี้คูณกันออกมาก็จะมีค่าเท่ากับ
M(AB) x ∂M(AB)/∂Q = Q x^(2)
พอเรานำไปแทนค่าในสมการในการคำนวณหาค่าการเสียรูปของคานก็ต้องไม่ลืมที่จะนำเทอมโมเมนต์ความเฉื่อยที่ขึ้นอยู่กับค่า x หรือ I(x) รวมไปในการวิเคราะห์โครงสร้างด้วย เพราะว่าค่า x ภายในสมการของค่าโมเมนต์ความเฉื่อยนั้นจะต้องถูก INTEGRATE ไปพร้อมกันด้วยนั่นเองครับ
พอทำเราทุกๆ อย่างตามขั้นตอนตามปกติแล้วก็จะทำให้ได้ค่าของคำตอบซึ่งมีค่าเท่ากับ
∆(ACTUAL) CASE 1 = 0.023 mm
ซึ่งหากเราทำการเปรียบเทียบค่า ∆ ที่คำนวณได้นี้กับค่า ∆ ที่ได้จาก EXACT EQUATION ของกรณีคานรับแรงดัดเป็นหลักที่มีค่าโมเมนต์ความเฉื่อยที่คงที่ ก็จะมีค่าเท่ากับ
∆ = P L^(3) / 3EI
หากดูจากรูปก็จะพบว่าค่าที่คำนวณได้นั้นจะมีความสอดคล้องกัน นั่นก็คือค่าที่คำนวณได้จะมีค่าใกล้เคียงกันกับค่า ∆(AVE) ซึ่งมีค่าเท่ากับ
∆(AVE) = 0.028 mm
และค่า ∆(ACTUAL) ก็จะมีค่าน้อยกว่าค่า ∆(MAX) และมากกว่าค่า ∆(MIN) แต่อย่างที่ผมได้นำเรียนไปตั้งแต่ตอนต้นนะครับว่า สำหรับกรณีของคานยื่นในปัญหาข้อนี้ คำตอบที่คำนวณได้นี้จะไม่ถูกต้อง กล่าวคือมีค่าความคลาดเคลื่อนออกไปจากค่าจริงๆ ที่ควรจะได้หลายเท่าตัวเลย
เอาเป็นว่าในวันพรุ่งนี้เรามาติดตามกันนะครับว่า หากเรานำเทอมของแรงเฉือนมาคำนึงถึงด้วย ค่าของคำตอบจริงๆ ที่ควรจะได้นั้นจะมีค่าที่เปลี่ยนแปลงไปมากหรือน้อยขนาดไหน หากว่าเพื่อนๆ ท่านใดที่มีความสนใจในหัวข้อๆ นี้เป็นพิเศษ ก็สามารถที่จะติดตามอ่านบทความของผมได้ครับ
หวังว่าความรู้เล็กๆ น้อยๆ ที่ผมได้นำมาฝากแก่เพื่อนๆ ทุกๆ ท่านในวันนี้จะมีประโยชน์ต่อทุกๆ ท่านไม่มากก็น้อย และ จนกว่าจะพบกันใหม่นะครับ
#ปัญหาและเทคนิคในการทำงานก่อสร้างโครงสร้างประเภทต่างๆ
#ปัญหาค่าความคลาดเคลื่อนของคำตอบที่ได้จากการวิเคราะห์หาค่าการเสียรูปของคานยื่นในกรณีที่คำนึงและไม่คำนึงถึงผลของการเสียรูปอันเนื่องมาจากแรงเฉือน
#การโพสต์ครั้งที่หนึ่ง
ADMIN JAMES DEAN
บริษัท ภูมิสยาม ซัพพลาย จำกัด ผู้นำกลุ่มธุรกิจเสาเข็มสปัน ไมโครไพล์ รายแรกและรายเดียวในประเทศไทย ที่ได้การรับรองมาตรฐาน ISO 45001:2018 การจัดการอาชีวอนามัยและความปลอดภัย การให้บริการตอกเสาเข็ม The Provision of Pile Driving Service และได้รับการรับรอง ISO 9001:2015 ของระบบ UKAS และ NAC รายแรกและรายเดียวในประเทศไทย ที่ได้รับการรับรองระบบบริหารงานคุณภาพ ตามมาตรฐานในกระบวนการ การออกแบบเสาเข็มสปันไมโครไพล์ การผลิตเสาเข็มสปันไมโครไพล์ และบริการตอกเสาเข็มเสาเข็มสปันไมโครไพล์ (Design and Manufacturing of Spun Micropile/Micropile and Pile Driving Service) Certified by SGS (Thailand) Ltd.
บริษัท ภูมิสยาม ซัพพลาย จำกัด คือผู้ผลิตรายแรกและรายเดียวในไทย ที่ได้รับการรับรองคุณภาพ Endoresed Brand จาก SCG ด้านการผลิตเสาเข็ม สปันไมโครไพล์ และได้รับเครื่องหมาย มาตรฐาน อุตสาหกรรม มอก. 397-2524 เสาเข็มสปันไมโครไพล์ Spun Micro Pile พร้อมรับประกันผลงาน และความเสียหายที่เกิดจากการติดตั้ง 7+ Year Warranty เสาเข็มมีรูกลมกลวงตรงกลาง การระบายดินทำได้ดี เมื่อตอกแล้วแรงสั่นสะเทือนน้อยมาก จึงไม่กระทบโครงสร้างเดิม หรือพื้นที่ข้างเคียง ไม่ต้องขนดินทิ้ง ตอกถึงชั้นดินดานได้ ด้วยเสาเข็มคุณภาพมาตรฐาน มอก. การผลิตที่ใช้เทคโนโลยีที่ทันสมัย จากประเทศเยอรมัน เสาเข็มสามารถทำงานในที่แคบได้ หน้างานสะอาด ไม่มีดินโคลน เสาเข็มสามารถรับน้ำหนักปลอดภัยได้ 15-50 ตัน/ต้น ขึ้นอยู่กับขนาดเสาเข็มและสภาพชั้นดิน แต่ละพื้นที่ ทดสอบโดย Dynamic Load Test ด้วยคุณภาพและการบริการที่ได้มาตรฐาน เสาเข็มเราจึงเป็นที่นิยมในงานต่อเติม
รายการเสาเข็มภูมิสยาม
1. สี่เหลี่ยม S18x18 cm.
รับน้ำหนัก 15-20 ตัน/ต้น
2. กลม Dia 21 cm.
รับน้ำหนัก 20-25 ตัน/ต้น
3. กลม Dia 25 cm.
รับน้ำหนัก 25-35 ตัน/ต้น
4. กลม Dia 30 cm.
รับน้ำหนัก 30-50 ตัน/ต้น
(การรับน้ำหนักขึ้นอยู่กับสภาพชั้นดินในแต่ละพื้นที่)
☎ สายด่วนภูมิสยาม:
082-790-1447
082-790-1448
082-790-1449
091-947-8945
081-634-6586
? Web:
bhumisiam.com
micro-pile.com
spun-micropile.com
microspunpile.com
bhumisiammicropile.com